Random Scientific Question

[Mike Rotch]

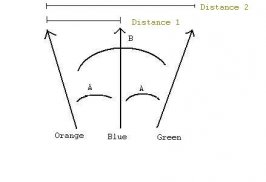
Consider 3 lines (as in the sketch below).

The angle between the left line - 'Orange' and the middle line - 'Blue', and the right line - 'Green' and the middle line - 'Blue' are equal (to "A").

The angle between Orange and Green is represented by "B". Obviously B=2A.

Now consider what would happen if all 3 lines were extended to infinity. Then the distance between Orange and Green, and Orange and Blue would have to be equal. 'Distance 1' would = 'Distance 2'!

Weird no? Or did I miss something?

 

[DQuaN]

Assuming that the middle line is perfectly vertical and the two lines on either side are at the same angle from the centre line then all numbers would be increased but their ratios to eachother will still be the same. i.e. Distance 1 will still be half that of Distance 2.

Although I am not sure what, exactly, you are asking.

 

[Mike Rotch]

Assuming that the middle line is perfectly vertical and the two lines on either side are at the same angle from the centre line then all numbers would be increased but their ratios to eachother will still be the same. i.e. Distance 1 will still be half that of Distance 2.

Although I am not sure what, exactly, you are asking.

I am asking whether I am correct.

But at a point at infinity, would their ratios to each other still be the same?

 

[scoobyonline200]

If they were streatched to infinity....then wouldnt the lines lay completley horizontal and become one.....where as they will only be one line???? I dont know much about science stuff but this is my take on this

 

[Famine]

Technically, yes. But consider the problem below:

Let x=y

Therefore x-y = 0

Therefore 2x - 2y = 2 (x-y) = 0

So 2 (x-y) = (x-y)

Divide throughout by (x-y)

2 = 1

You run into the same basic theoretical problem. Multiplying by infinity (which is what "Distance 1" becomes) is the same as dividing by zero (which is, after all, what you're asked to do when you cancel out the (x-y) in the above sum) - both are mathematically impossible. Although the sums are borne out by the algebraic proof, neither has any meaning when converted into numbers.

 

[the_cobbinator]

Nice, simple explanation, Famine.

 

[Danoff]

Technically, yes. But consider the problem below:

Let x=y

Therefore x-y = 0

Therefore 2x - 2y = 2 (x-y) = 0

So 2 (x-y) = (x-y)

Divide throughout by (x-y)

2 = 1

The part where you say divide through by (x-y)... you can't do that. x-y is zero and you can't divide by zero. But I suspect you knew that.


Anyway the thing about the lines.... the distances will never be equal. They don't go to infinity at the same rate. Besides which, infinity is not a number so you can't use it the way you're using it.

 

[Solid Lifters]

Nice, simple explanation, Famine.

Simple? Says you!

 

[Ev0]

Math and summertime don't mix

But I don't get what you're saying, Mike. Is this something that would require a knowledge of calculus, because logic would dictate that if the angles remain the same, the ratio between distance 1 and 2 should remain the same as long as the lines remain straight. I'd like to see the math that proves what you're saying (if I can understand it, I am taking calculus in September hopefully).

*edit* after thinking about it more, if the lines are infinite then of course the two distances would be infinite too, meaning that they are in essence the same distance, yet the ratio would still be the same... tricky problem, calculus would probably give a definite answer though.

 

[Mike Rotch]

But I don't get what you're saying, Mike. Is this something that would require a knowledge of calculus, because logic would dictate that if the angles remain the same, the ratio between distance 1 and 2 should remain the same as long as the lines remain straight. I'd like to see the math that proves what you're saying (if I can understand it, I am taking calculus in September hopefully).

*edit* after thinking about it more, if the lines are infinite then of course the two distances would be infinite too, meaning that they are in essence the same distance, yet the ratio would still be the same... tricky problem, calculus would probably give a definite answer though.

Your edit part is what I was getting at, but as Famine and danoff said, using infinity as a number is a no-no.

 

[Famine]

The part where you say divide through by (x-y)... you can't do that. x-y is zero and you can't divide by zero. But I suspect you knew that.

Indeed - and I specifically stated that in my post and used it to underline the reason why the answer to Mike's problem is what it is.

But I suspect you knew that.

 

[Event]

All of our understanding of math, science, and everything breaks down at infinity. It cannot be explained.

 

[Nick_Johnston28]

In the end, no matter how long each line is (as long as they are equal) distance 1 would be half of distance 2, right?

 

[Jay]

Yeah but distance 1 would be infinity and distance 2 would also be infinity, So they are equal.

 

[Nick_Johnston28]

Infinity isn't a number, if they go on forever (which they do,the little ^ signs say so ) there has to be a number, even if it's say, 123,352,135,274,345,913,563,235,323 , there will always be a number.

 

[Arwin]

All of our understanding of math, science, and everything breaks down at infinity. It cannot be explained.

I tend to agree with Nick. It depends on how you look at infinity. In my view, it's just used wrong here. Infinity is the lack of limits. In other words, there is no endpoint and thus infinity can never actually be reached. So you cannot ask the question Mike is asking, because that situation can never occur - the lines can and will never reach infinity, can never be stretched to infinity, they can only be infinitely stretched. Subtle difference, but an important one.

I by the way think you can actually divide by zero, it's just that the answer is infinity so it has the same theoretical status and can never actually be performed.

 

[Sage]

I think infinity's a definition more than anything... look at zero for instance. Zero can't possibly exist, because if it did, then it wouldn't be zero anymore! Zero is simply a placeholder, and a definition of that which doesn't exist. And anyway, infinity's a useful concept... doing limits with really big numbers would be silly (instead of just using as x approaches infinity).

 

[Nick_Johnston28]

I think infinity's a definition more than anything... look at zero for instance. Zero can't possibly exist, because if it did, then it wouldn't be zero anymore! Zero is simply a placeholder, and a definition of that which doesn't exist. And anyway, infinity's a useful concept... doing limits with really big numbers would be silly (instead of just using as x approaches infinity).

What does infinity equal then? if x=infinity and b= 1/2 x , what does B equal?

 

[Event]

Infinity can't be a number and therefor it cannot be used in algebraic equations.

 

[Sage]

Exactly. You can't algebraically manipulate infinity... it's a concept, not a number, and not even an imaginary number. If you add 1 to infinity (impossible to begin with), you end up with infinity... if you subtract 1 from infinity (again, impossible to begin with), you still end up with infinity. It's purely conceptual for calculus and physics purposes. Even in calculus and physics, you don't manipulate it.

 

[Ev0]

So I guess infinity is sort of like zero, in the sense that it is not a real number and is actually a concept. They are just opposites of eachother, zero being nothing and infinity being 'bigger than big' to really dumb it down (I'm too lazy to come up with a better explination).

 

[Event]

So I guess infinity is sort of like zero, in the sense that it is not a real number and is actually a concept. They are just opposites of eachother, zero being nothing and infinity being 'bigger than big' to really dumb it down (I'm too lazy to come up with a better explination).

They are still very unlike eachother. You can use 0 in algebraic equations. add 1 to 0 and you have 1. Subtract 1 from 0 and you have -1. Infinity cannot do that.

 

[Arwin]

I think Ev0 put it pretty well. -1 isn't more real than infinity. You can't hold one icecream, take 2 away and say you now have -1 icecreams in your hand. In that respect, infinity and zero are really theoretical opposites of a scale. But we can use negative numbers to represent a change, for instance from 2 to 1, in which case we represent the change as -1, i.e. one being removed. Because of that, we can deal with the concept of 0-1, completely forgetting that this, in fact, is as impossible as subtracting 1 from infinity. Just at this moment we have less trouble finding use for it.

At least, that's my take on it. I am by no means a mathematician though.

 

[Event]

The one theoretical number, like infinity, that is opposite of infinity is not zero, it is infinitessimal. The opposite of 0 is 1. the absencse of something vs. the presence of something. Infintessimal (this is an adjective, I don't know the noun) is the smallest amount of something you can have without not having it.

 

[Omero]

I have a theory regarding theoretical values of nonreal numbers. It says that 0 = infinity or they coincide somehow. For example, through deductive reasoning I have determined that a number divided by 0 is equal to infinity (it works. Infinity has no value; it has no end or definition. When dividing a number by zero, it's like taking the lack of an end and turning it around to face the lesser values because ten parts of 0 makes the 0 an insanely small number; infinitely small. Therefore 10/0 = infinity). The same thing works when multiplying a number by infinity (only backwards). It is complicated and confuses me to no end. However, back to the question.

In order to have a measurable segment of a line, there must be two defined points. So, in making and measuring the distance between the lines, you have to give it a real value (we'll say Q for the variable name). In extending the segment to the opposite line, using the geometrical theorems regarding triangles, it must be that the extended line is twice the length of the non-extended line (in measuring it, you eliminated the factor of infinity).