You should ALL go buy Skip Barbers book, Going Faster and read the chapter on tires. Especially you, Scaff.
What you say in this thread is mostly true, and for that you are to be congratulated. But you should have sprinkled a little sugar on what you say about weight not being significant to stopping distance because you are wrong, and your pedantic tone is about to be shoved back down your throat. (please to excuse)

***What you and your referenced materials miss is that the CF (coefficient of friction) is NOT a constant, it is a function of load applied***
Heinlein once wrote that people who dont understand mathematics are just little apes. So heres the math:
Relevant formula:
A1 = F1/m1
A2 - F2/m2
F = u * F,
F = m * g
Where A1 is the deceleration, F1 is the force applied, and m1 is the mass of car 1. Ditto for A2, F2, m2. F is frictional force, u is the CF, and F is the normal force on the object in question (in this case, downward). Lets assume this is a car with only one wheel and one tire, in order to eliminate weight transfer as a factor (for the moment).
What you are saying is that A1 = A2 because F1 and F2 are proportional to m1 and m2. (i.e., A = u*m*g / m, therefore, A = u*g, a constant! All hail Galileo!) 👍 This is true as long as u is a constant.
But, u is NOT a constant. This is the assumption that practically every high school science teacher (and college professor) who doesnt understand tire physics makes. (how did you make this mistake??) u, CF, is a function of many variables including slip angle, percent slip (static vs. dynamic friction, a whole nother ball of wax), tire temperature, track temperature, tire material, track material, AND weight.
Yes, weight. And yes, while it is true that CF sometimes INCREASES as load increases. It only increases at very low normal forces and then decreases! And it doesnt decrease linearly. Ill have to scan in Skip Barbers graph, but it looks basically like this:
Maximum static CF vs. Load (edited after looking at the book
)

Why is this? Well, tire manufacturers write heavy volumes about that subject, but essentially, its because nothing is unbreakable. Just think of a rubber eraser. You rub very lightly, and there is almost no friction. You push harder, and you get lots of friction mostly due to a larger contact patch (the rubber bites into the paper and the graphite markings are lifted up). You push really hard, and the eraser material breaks down, and you get slippage, shredded paper, and rolling on those wee little bits of broken off eraser bits.
(edit: this site has interesting pictures backing up the above statements:
http://www.insideracingtechnology.com/tirebkexerpt1.htm)
So, imagine you have a car (a) with a mass 1000kg, CF of 1.2. It will have a frictional force of 12,000Newtons, and decelerate at 1.2g (12m/s^2). And, if you have a heavier car (b) 1500kg with CF of 1.1, it will have a larger frictional force, 16,500N, and decelerate slower at 1.1g. And, if you take a third car (c), one that is too heavy, mass 2000kg, the CF decreases to 0.9 (your tires are starting to fail). While the friction is larger, 18,000N (I hope your 71 VW Bugs brakes can handle this good luck), the deceleration is less, 0.9g. (do the math) We could write a formula fitting the u function, but I dont think thats necessary is it?
Now of course, the graph I drew here is just an idealized theoretical one (and doesnt even take into account dynamic sliding CF (~30% less than static friction CF), which I would hazard to guess is also a function of normal force, amongst other factors), and RL tires are far more complex, but they ALL follow this basic curve.
You can get this info for different RL tires from the manufacturers (maybe), or you can look in Skip Barbers book (how do you like my ad homonym appeals to authority? Eh? My Skip Barber can beat up your professional physicist, amateur racer). Weight transfer will not help you, because you transfer force to the front tires you remove it from the rear tires in proportion to the rate of deceleration, the distance of the CG from the front tires, and the CGs height above the ground.
Ftransfer = a * m * h / L
Where Ftransfer is the force transferred, a is the rate of deceleration, m is the mass of the car, h is the height, and L is the length from wheel to CG. (see Skip, p. 204)
So for our two cars (m1 and m2), h and L are the same. Ftransfer proportional to a * m. If the two cars decelerate at the same a, then the more massive car would have a larger Ftransfer.
If m2 > m1, then
Ftransfer2 > Ftransfer1
Since a greater Ftransfer leads to a smaller CF, the larger car has a proportionally lower F. And you can see the example cars a, b, and c apply.
To summarize: assuming all other things being equal (car type, tire type, brake power, aerodynamics, suspension, CG location, etc) a heavier car will decelerate LESS THAN a lighter car.
Size matters.
Case closed.
yeah right


(please note, I'm sorry for the flame, but you've got me on tilt. Also, you are absolutely correct in saying that the tires are the MOST IMPORTANT factor in braking. You are just plain wrong about the idea that weight is not relevant. And in this case, every 5yr old kid knows it, and is actually right. Tho, he thinks it for the wrong reason... but let's not get into that...)






 🤬 🤬 🤬
🤬 🤬 🤬
 call some of your detractors apes -- those other posters who do not make any attempt at understanding the underlining math. You clearly understand the math. 'nuff said.
call some of your detractors apes -- those other posters who do not make any attempt at understanding the underlining math. You clearly understand the math. 'nuff said.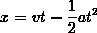


 [shrug]
[shrug]